Formula Ownage

Here are my own notes for keeping on top of the consistency and balance of formulas.

Consistency

you want to own the formula, you don't want it to own you, so you have to make sure it behaves how you want for all the conditions the formula allows (based on it's independent parameters)

For instance, if you're making a formula for a roll based on multiple attributes, you'll want to consider the case of the balanced character, the physical character, the magic character, the dexterous character.

Balance

We also don't want our formulas for the fighter's physical skills to grow faster than the formulas for the mage's magical skills. This is tough to factor in, since the mage can cause effects on their opponents that don't exactly equate to damage. This is why you have lots of handy expressions in formulas that can be used to manipulate it for your needs.

Tools

Here are some handy expressions and concepts to wreak pwnge on your equations:

Constants

constants are handy for scaling. Whether they're in front of a term or buried inside a me complex expression, they can help bring balance to an equation. For instance, if you have a skill that relies more on dexterity than strength, but you want it to rely on both, you can make the success go as:

S = a*str + b*str

where a and b are arbitrary constants that you can scale to strengthen the growth of a particular term In our case, we could take (a = 1) and (b = 2) to make strength dominate the equation

Function behavior

maximums

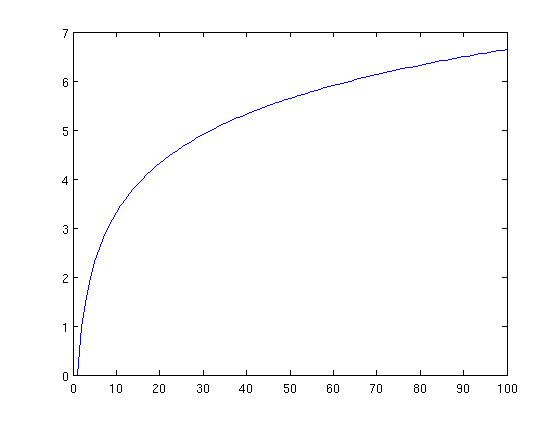
if you want your formula to stop climbing after a certain point, the logarithm is ideal. The logarithm climbs fast when the dependent variables are closer to 0, but as they approach a given value (depending on what base you chose for the log) they begin to climb much slower as the function levels out. It has the form:

y = log(x)

here's a base 2 log function.

Comment: Note that this function doesn't really has a maximum. It will reach any y-value at some point. As an alternative I would recommend using a function of the form y = a - a / (x + 1). This results in a function that approaches a but never reaches it. --Crush 11:49, 5 November 2007 (CET)

here's the formula Crush suggested if it more fits your needs:

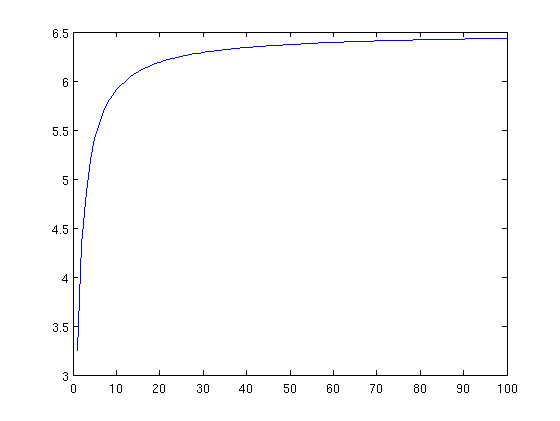
Yeah, I thought about this. Since everything here should be numerical it shouldn't be a problem. But your formula is probably more user-friendly because you don't have to figure out what base to use for your log function; instead your max is simply decided by "a". The thing about -a/x is after it hits the "bend" it doesn't increase much anymore, whereas at higher levels, the characters will still get gains from the logarithmic function (just not as large of gains). I need to rename this section something besides "maximum" but I want it to be intuitive to non-math peoples." --Zao 4:10 5 November 2007 (CET)

exponentials

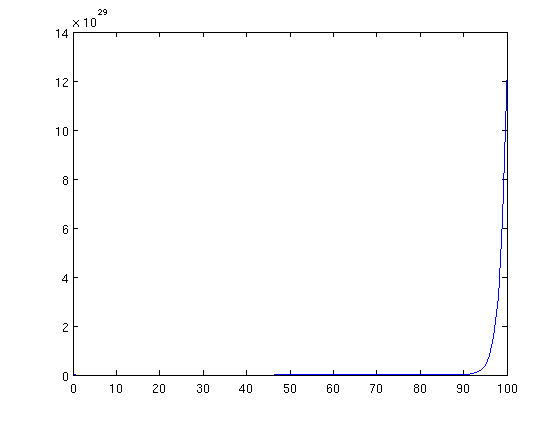
exponentials climb or fall really fast. They have the form:

y = c^x

where c is an arbitrary constant greater than |1|

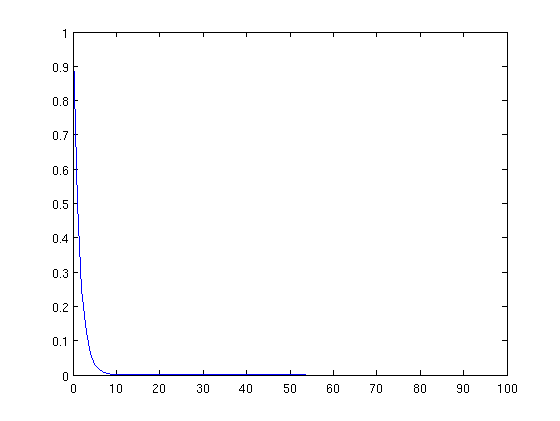
I can't think of a use for them off the top of my head in a game, but here's what the positive one looks like:

and a negative: