(Added the Circle-Sector with Disk collision) |
m (Final touch...) |
||
| Line 7: | Line 7: | ||
== Circle-Sector with Disk == | == Circle-Sector with Disk == | ||
''By [[User:Avaniel|Avaniel]] 20:37, 27 February 2007 (CET)'' | |||
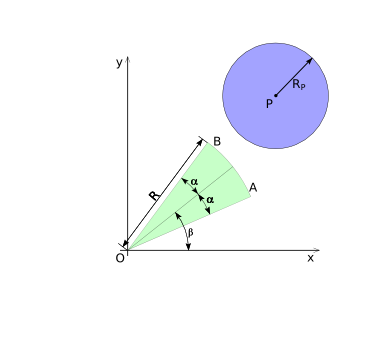
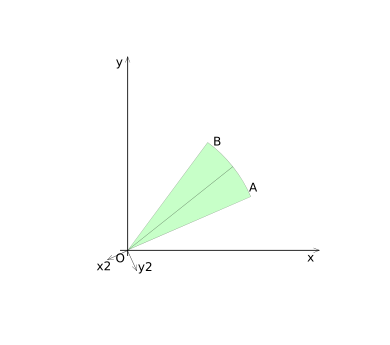
In order to determine if a circle-sector and a disk collide, we start with transforming the coordinates of the 2d space in such a way that the center of the circle-sector is located at the origin. The circle-sector can then be defined by a radius ''R'', a half-top-angle ''alpha'' and a placement angle ''beta'', as shown in diagram (1). | In order to determine if a circle-sector and a disk collide, we start with transforming the coordinates of the 2d space in such a way that the center of the circle-sector is located at the origin. The circle-sector can then be defined by a radius ''R'', a half-top-angle ''alpha'' and a placement angle ''beta'', as shown in diagram (1). | ||
| Line 12: | Line 13: | ||
The disk can simply be defined by its center-point ''P'' and its radius ''R<sub>P</sub>'', where point ''P'' can be anywhere in the 2d space. See diagram (CSD-1) for an overview. | The disk can simply be defined by its center-point ''P'' and its radius ''R<sub>P</sub>'', where point ''P'' can be anywhere in the 2d space. See diagram (CSD-1) for an overview. | ||
[[Image:Collision-circlesecor-disk-dimensions.png|frame|none|Diagram (CSD-1)]] | [[Image:Collision-circlesecor-disk-dimensions.png|frame|none|Diagram (CSD-1) - Overview of the Circle-Sector and Disk]] | ||
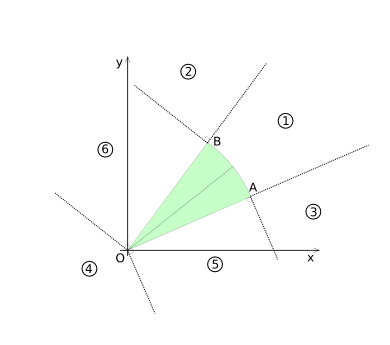
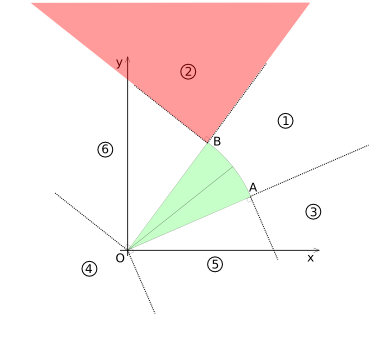
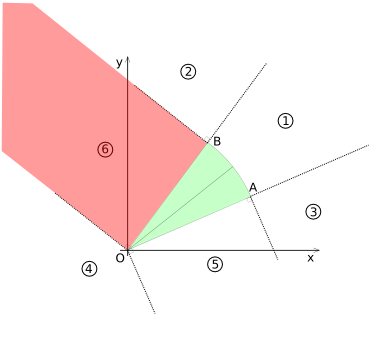
In order to determine if the circle-sector and the circle intersect, the x-y plane is | In order to determine if the circle-sector and the circle intersect, the x-y plane is divided in 6 ''Voronoi'' like regions. The regions are based on the vertexes ''O-A'', ''O-B'' and the arc ''A-B''. They are shown in diagram (CSD-2). | ||
[[Image:Collision-circlesecor-disk-voronoi.png|frame|none|Diagram (CSD-2)]] | [[Image:Collision-circlesecor-disk-voronoi.png|frame|none|Diagram (CSD-2) - The x-y plane divide in 6 'Voronoi' regions]] | ||
For each region it is now determined what the pre-conditions for an overlap are, if ''P'' is in that region. If necessary, the pre-conditions for point ''P'' being in the region will be derived as well. | For each region it is now determined what the pre-conditions for an overlap are, if ''P'' is in that region. If necessary, the pre-conditions for point ''P'' being in the region will be derived as well. | ||
| Line 25: | Line 26: | ||
=== Region 1 === | === Region 1 === | ||
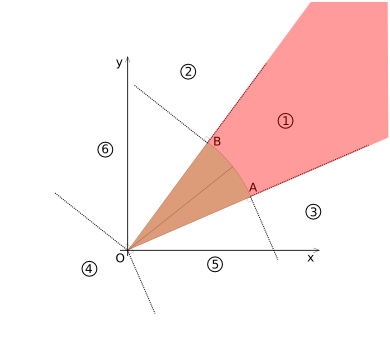
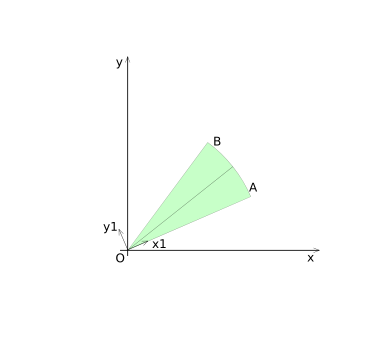
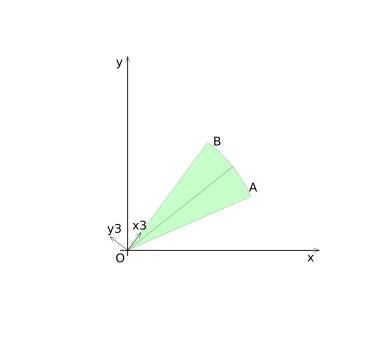
Region 1 is highlighted in diagram (CSD-3), it includes the interior of the Circle-sector. For region 1, the coordinates for point ''P'' are transformed to coordinate system 1 (shown in diagram (CSD-4)). | Region 1 is highlighted in diagram (CSD-3), it includes the interior of the Circle-sector. For region 1, the coordinates for point ''P'' are transformed to coordinate system 1 (shown in diagram (CSD-4)). [[:Image:Collision-circlesecor-disk-example1.png|An example of a region 1 collision is give here.]] | ||
[[Image:Collision-circlesecor-disk-voronoi1.png|frame|none|Diagram (CSD-3)]] | [[Image:Collision-circlesecor-disk-voronoi1.png|frame|none|Diagram (CSD-3) - 'Voronoi' region 1 highlighted]] | ||
[[Image:Collision-circlesecor-disk-axis1.png|frame|none|Diagram (CSD-4)]] | [[Image:Collision-circlesecor-disk-axis1.png|frame|none|Diagram (CSD-4) - Coordinate system 1]] | ||
The coordinates for point ''P'' in coordinate system 1 are: | The coordinates for point ''P'' in coordinate system 1 are: | ||
| Line 45: | Line 46: | ||
Point ''P'' is inside region 1 if | Point ''P'' is inside region 1 if | ||
:P<sub>x1</sub> >= 0 , P<sub>y1</sub> >= 0 and P<sub>y1</sub> <= P<sub>x1</sub> tan(2alpha) | :P<sub>x1</sub> >= 0 , P<sub>y1</sub> >= 0 and P<sub>y1</sub> <= P<sub>x1</sub> tan(2alpha) = P<sub>x1</sub> {2sin(alpha)cos(alpha) / (cos<sup>2</sup>(alpha) - sin<sup>2</sup>(alpha))} | ||
The Circle-sector and the disc then intersect if | The Circle-sector and the disc then intersect if | ||
| Line 54: | Line 55: | ||
=== Region 2 === | === Region 2 === | ||
Region 2 is highlighted in diagram (CSD-5). For this region no coordinate transformations are necessary. | Region 2 is highlighted in diagram (CSD-5). For this region no coordinate transformations are necessary. [[:Image:Collision-circlesecor-disk-example2.png|An example of a region 2 collision is give here.]] | ||
[[Image:Collision-circlesecor-disk-voronoi2.png|frame|none|Diagram (CSD-5)]] | [[Image:Collision-circlesecor-disk-voronoi2.png|frame|none|Diagram (CSD-5) - 'Voronoi' region 2 highlighted]] | ||
If point ''P'' is inside region 2, the circle-sector and the disk can only intersect if point ''B'' is inside the circle. | If point ''P'' is inside region 2, the circle-sector and the disk can only intersect if point ''B'' is inside the circle. | ||
| Line 73: | Line 74: | ||
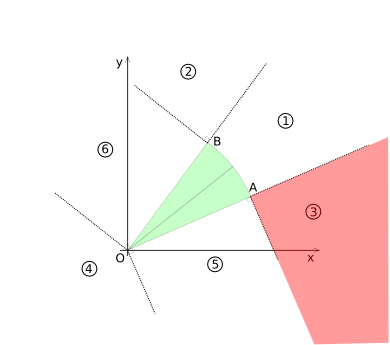
=== Region 3 === | === Region 3 === | ||
Region 3 is highlighted in diagram (CSD-6). For this region no coordinate transformations are necessary. | Region 3 is highlighted in diagram (CSD-6). For this region no coordinate transformations are necessary. [[:Image:Collision-circlesecor-disk-example3.png|An example of a region 3 collision is give here.]] | ||
[[Image:Collision-circlesecor-disk-voronoi3.png|frame|none|Diagram (CSD-6)]] | [[Image:Collision-circlesecor-disk-voronoi3.png|frame|none|Diagram (CSD-6) - 'Voronoi' region 3 highlighted]] | ||
Analogous to region 2, the circle-sector and the disk can only intersect if point ''A'' is inside the disk. The condition for this is: | Analogous to region 2, the circle-sector and the disk can only intersect if point ''A'' is inside the disk. The condition for this is: | ||
| Line 92: | Line 93: | ||
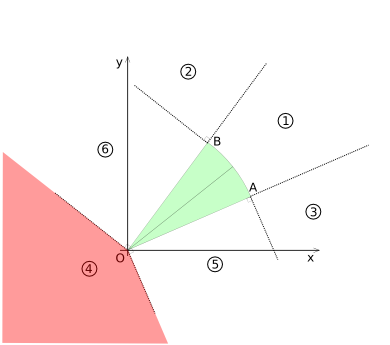
=== Region 4 === | === Region 4 === | ||
Region 4 is highlighted in diagram (CSD-7). For this region no coordinate transformations are necessary. | Region 4 is highlighted in diagram (CSD-7). For this region no coordinate transformations are necessary. [[:Image:Collision-circlesecor-disk-example4.png|An example of a region 4 collision is give here.]] | ||
[[Image:Collision-circlesecor-disk-voronoi4.png|frame|none|Diagram (CSD-7)]] | [[Image:Collision-circlesecor-disk-voronoi4.png|frame|none|Diagram (CSD-7) - 'Voronoi' region 4 highlighted]] | ||
Analogous to regions 2 and 3, the circle-sector and the disk can only intersect if point ''O'' is inside the disk. The condition for this is: | Analogous to regions 2 and 3, the circle-sector and the disk can only intersect if point ''O'' is inside the disk. The condition for this is: | ||
| Line 103: | Line 104: | ||
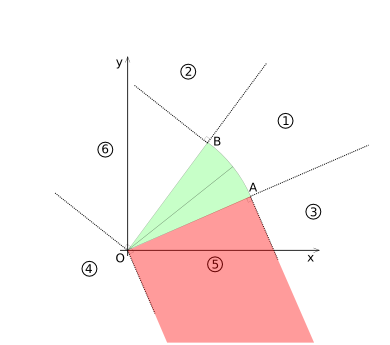
=== Region 5 === | === Region 5 === | ||
Region 5 is highlighted in diagram (CSD-8). For region 5, the coordinates for point ''P'' are transformed to coordinate system 2 (shown in diagram (CSD-9)). | Region 5 is highlighted in diagram (CSD-8). For region 5, the coordinates for point ''P'' are transformed to coordinate system 2 (shown in diagram (CSD-9)). [[:Image:Collision-circlesecor-disk-example5.png|An example of a region 5 collision is give here.]] | ||
[[Image:Collision-circlesecor-disk-voronoi5.png|frame|none|Diagram (CSD-8)]] | [[Image:Collision-circlesecor-disk-voronoi5.png|frame|none|Diagram (CSD-8) - 'Voronoi' region 5 highlighted]] | ||
[[Image:Collision-circlesecor-disk-axis2.png|frame|none|Diagram (CSD-9)]] | [[Image:Collision-circlesecor-disk-axis2.png|frame|none|Diagram (CSD-9) - Coordinate system 2]] | ||
In the local coordinates the following conditions for ''P'' being in region 5, can be formulated: | In the local coordinates the following conditions for ''P'' being in region 5, can be formulated: | ||
| Line 139: | Line 140: | ||
=== Region 6 === | === Region 6 === | ||
Region 6 is highlighted in diagram (CSD-10). For region 6, the coordinates for point ''P'' are transformed to coordinate system 3 (shown in diagram (CSD-11)). | Region 6 is highlighted in diagram (CSD-10). For region 6, the coordinates for point ''P'' are transformed to coordinate system 3 (shown in diagram (CSD-11)). [[:Image:Collision-circlesecor-disk-example6.png|An example of a region 6 collision is give here.]] | ||
[[Image:Collision-circlesecor-disk-voronoi6.png|frame|none|Diagram (CSD-10)]] | [[Image:Collision-circlesecor-disk-voronoi6.png|frame|none|Diagram (CSD-10) - 'Voronoi' region 6 highlighted]] | ||
[[Image:Collision-circlesecor-disk-axis3.png|frame|none|Diagram (CSD-11)]] | [[Image:Collision-circlesecor-disk-axis3.png|frame|none|Diagram (CSD-11) - Coordinate system 3]] | ||
In the local coordinates the following conditions for ''P'' being in region 6, can be formulated: | In the local coordinates the following conditions for ''P'' being in region 6, can be formulated: | ||
| Line 169: | Line 170: | ||
=== The Algorithm === | === The Algorithm === | ||
The following values need to be given; the radius of the circle-sector | The following values need to be given; the radius of the circle-sector ''R'', the half-top-angle ''alpha'', the placement angle ''beta'', the coordinates of the center of the circle-sector, the coordinates of the center of the disk ''P'' and the radius of the disk ''R<sub>P</sub>''. | ||
* Subtract the coordinates of the center of the circle sector from the coordinates of point ''P''. | * Subtract the coordinates of the center of the circle sector from the coordinates of point ''P''. | ||
* Check for a region 4 intersection. | * Check for a region 4 intersection. | ||
| Line 177: | Line 178: | ||
* Calculate the coordinates of point ''B''. | * Calculate the coordinates of point ''B''. | ||
* Check for a region 2 intersection. | * Check for a region 2 intersection. | ||
* Calculate the coordinates of point | * Calculate the coordinates of point ''P'' in coordinate system 2. | ||
* Check for a region 5 intersection. | * Check for a region 5 intersection. | ||
* Calculate the coordinates of point | * Calculate the coordinates of point ''P'' in coordinate system 3. | ||
* Check for a region 6 intersection. | * Check for a region 6 intersection. | ||
* Calculate the coordinates of point | * Calculate the coordinates of point ''P'' in coordinate system 1. | ||
* Check for a region 1 intersection. | * Check for a region 1 intersection. | ||
Any but the first three steps can be moved, if that is found to be more appropriate. | Any but the first three steps can be moved, if that is found to be more appropriate. The algorithm includes 4 calls to a trigonomic function and just 1 division. | ||
In the current combat implementation sin(beta) and cos(beta) do not need to be calculated at runtime. ''Beta'' is determined by the direction the attacker is facing. There are only four possible values for ''beta''; 0, pi/2, pi and pi*3/2. Because the half-top-angle is a property of the weapon used, sin(alpha) | In the current combat implementation sin(beta) and cos(beta) do not need to be calculated at runtime. ''Beta'' is determined by the direction the attacker is facing. There are only four possible values for ''beta''; 0, pi/2, pi and pi*3/2. Because the half-top-angle is a property of the weapon used, sin(alpha), cos(alpha) and tan(2alpha) could be computed on startup of the game-server and stored for use. | ||
Revision as of 19:37, 27 February 2007
This article is currently only a proposal
The features or design guidelines described in this article are only a proposal made by one or some persons. It has not been evaluated or accepted by the core development team yet. Feel free to add your personal opinion about them or make counter proposals.
This page was created to document the collision detection algorithms used in The Mana World. After the algorithms are converted to C++ and added to the code base it is very difficult to verify the assumptions and math of the author. Therefore an explanation of the algorithms used, is given below. Of course any improvements or clarifications can allso be added and discussed on this page.
Strictly speaking, the algorithms discussed here, compute if two geometric figures intersect. However, the result is then used in a dynamic game. In the game world two objects will collide if their movement areas intersect.
Circle-Sector with Disk
By Avaniel 20:37, 27 February 2007 (CET)
In order to determine if a circle-sector and a disk collide, we start with transforming the coordinates of the 2d space in such a way that the center of the circle-sector is located at the origin. The circle-sector can then be defined by a radius R, a half-top-angle alpha and a placement angle beta, as shown in diagram (1).
The disk can simply be defined by its center-point P and its radius RP, where point P can be anywhere in the 2d space. See diagram (CSD-1) for an overview.
In order to determine if the circle-sector and the circle intersect, the x-y plane is divided in 6 Voronoi like regions. The regions are based on the vertexes O-A, O-B and the arc A-B. They are shown in diagram (CSD-2).
For each region it is now determined what the pre-conditions for an overlap are, if P is in that region. If necessary, the pre-conditions for point P being in the region will be derived as well.
In the following text, a subscript x and y are used to indicate x and y coordinate of a point. If the coordinates considered are in a tranformed coordinate system, an extra indicator will be added. For example the x-coordinate of point A in the x1-y1 coordinate system is denoted as: Ax1
Region 1
Region 1 is highlighted in diagram (CSD-3), it includes the interior of the Circle-sector. For region 1, the coordinates for point P are transformed to coordinate system 1 (shown in diagram (CSD-4)). An example of a region 1 collision is give here.
The coordinates for point P in coordinate system 1 are:
- Px1 = Px cos(beta-alpha) + Py sin(beta-alpha)
- Py1 = Py cos(beta-alpha) - Px sin(beta-alpha)
Using goniometric relations this can be simplified to:
- Px1 = Px {cos(alpha)cos(beta) + sin(alpha)sin(beta)} + Py {-sin(alpha)cos(beta) + cos(alpha)sin(beta)}
- Py1 = Py {cos(alpha)cos(beta) + sin(alpha)sin(beta)} - Px {-sin(alpha)cos(beta) + cos(alpha)sin(beta)}
Point P is inside region 1 if
- Px1 >= 0 , Py1 >= 0 and Py1 <= Px1 tan(2alpha) = Px1 {2sin(alpha)cos(alpha) / (cos2(alpha) - sin2(alpha))}
The Circle-sector and the disc then intersect if
- Px2 + Px2 <= (R + RP)2
Region 2
Region 2 is highlighted in diagram (CSD-5). For this region no coordinate transformations are necessary. An example of a region 2 collision is give here.
If point P is inside region 2, the circle-sector and the disk can only intersect if point B is inside the circle.
- (Px - Bx)2 + (Py - By)2 <= RP2
The coordinates of point B are:
- Bx = R cos(alpha + beta) = R {cos(alpha)cos(beta) - sin(alpha)sin(beta)}
- By = R sin(alpha + beta) = R {sin(alpha)cos(beta) + cos(alpha)sin(beta)}
With the coordinates for B the condition can now be evaluated.
Region 3
Region 3 is highlighted in diagram (CSD-6). For this region no coordinate transformations are necessary. An example of a region 3 collision is give here.
Analogous to region 2, the circle-sector and the disk can only intersect if point A is inside the disk. The condition for this is:
- (Px - Ax)2 + (Py - Ay)2 <= RP2
The coordinates of point A are:
- Ax = R cos(-alpha + beta) = R {cos(alpha)cos(beta) + sin(alpha)sin(beta)}
- Ay = R sin(-alpha + beta) = R {-sin(alpha)cos(beta) + cos(alpha)sin(beta)}
With the coordinates for A the condition can now be evaluated.
Region 4
Region 4 is highlighted in diagram (CSD-7). For this region no coordinate transformations are necessary. An example of a region 4 collision is give here.
Analogous to regions 2 and 3, the circle-sector and the disk can only intersect if point O is inside the disk. The condition for this is:
- Px2 + Py2 <= RP2
Region 5
Region 5 is highlighted in diagram (CSD-8). For region 5, the coordinates for point P are transformed to coordinate system 2 (shown in diagram (CSD-9)). An example of a region 5 collision is give here.
In the local coordinates the following conditions for P being in region 5, can be formulated:
- Px2 <= 0, Px2 >= -R and Py2 >= 0
The condition for the circle-sector and the disk intersecting is:
- Py2 <= RP
The coordinates for P in coordinate system 2 are given by:
- Px2 = Pxcos(alpha + beta + pi) + Pysin(alpha + beta + pi)
- Py2 = Pycos(alpha + beta + pi) - Pxsin(alpha + beta + pi)
Using the goniometric relations to handle the pi term first, the coordinates become:
- Px2 = -Pxcos(alpha + beta) + Pysin(alpha + beta )
- Py2 = -Pycos(alpha + beta) - Pxsin(alpha + beta )
Now using the goniometric relations to seperate alpha and beta:
- Px2 = -Px{cos(alpha)cos(beta) - sin(alpha)sin(beta)} + Py{sin(alpha)cos(beta) + cos(alpha)sin(beta)}
- Py2 = -Py{cos(alpha)cos(beta) - sin(alpha)sin(beta)} - Px{sin(alpha)cos(beta) + cos(alpha)sin(beta)}
The conditions can now be evaluated.
Region 6
Region 6 is highlighted in diagram (CSD-10). For region 6, the coordinates for point P are transformed to coordinate system 3 (shown in diagram (CSD-11)). An example of a region 6 collision is give here.
In the local coordinates the following conditions for P being in region 6, can be formulated:
- Px3 >= 0, Px3 <= R and Py3 >= 0
The condition for the circle-sector and the disk intersecting is:
- Py3 <= RP
The coordinates for P in coordinate system 3 are given by:
- Px3 = Pxcos(alpha + beta) + Pysin(alpha + beta)
- Py3 = Pycos(alpha + beta) - Pxsin(alpha + beta)
Now using the goniometric relations to seperate alpha and beta:
- Px3 = Px{cos(alpha)cos(beta) - sin(alpha)sin(beta)} + Py{sin(alpha)cos(beta) + cos(alpha)sin(beta)}
- Py3 = Py{cos(alpha)cos(beta) - sin(alpha)sin(beta)} - Px{sin(alpha)cos(beta) + cos(alpha)sin(beta)}
The conditions can now be evaluated.
The Algorithm
The following values need to be given; the radius of the circle-sector R, the half-top-angle alpha, the placement angle beta, the coordinates of the center of the circle-sector, the coordinates of the center of the disk P and the radius of the disk RP.
- Subtract the coordinates of the center of the circle sector from the coordinates of point P.
- Check for a region 4 intersection.
- Calculate sin(alpha), cos(alpha), sin(beta) and cos(beta) and store them in temporary variables.
- Calculate the coordinates of point A.
- Check for a region 3 intersection.
- Calculate the coordinates of point B.
- Check for a region 2 intersection.
- Calculate the coordinates of point P in coordinate system 2.
- Check for a region 5 intersection.
- Calculate the coordinates of point P in coordinate system 3.
- Check for a region 6 intersection.
- Calculate the coordinates of point P in coordinate system 1.
- Check for a region 1 intersection.
Any but the first three steps can be moved, if that is found to be more appropriate. The algorithm includes 4 calls to a trigonomic function and just 1 division.
In the current combat implementation sin(beta) and cos(beta) do not need to be calculated at runtime. Beta is determined by the direction the attacker is facing. There are only four possible values for beta; 0, pi/2, pi and pi*3/2. Because the half-top-angle is a property of the weapon used, sin(alpha), cos(alpha) and tan(2alpha) could be computed on startup of the game-server and stored for use.